UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL

INSTITUTO DE FÍSICA

MESTRADO PROFISSIONALIZANTE EM ENSINO DE FÍSICA

VIAGEM INTERPLANETÁRIA[1]

Trabalho apresentado à Prof. Dra Maria de Fátima Saraiva, na disciplina MEF008 - Ensino de Astronomia, do curso Mestrado Profissional em Ensino de Física do Instituto de Física da UFRGS.

ADRIANA RICHIT

MAURI LUIS TOMKELSKI

Porto Alegre, Agosto de 2003

VIAGEM INTERPLANETÁRIA

Nesta experiência você fará parte de uma viagem tripulada para Marte. Assim, você aprenderá sobre órbitas, períodos e velocidades de planetas naturais e naves espaciais.

1. ÓRBITA E PERÍODOS PLANETÁRIOS

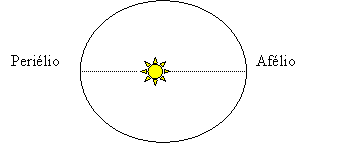
Abaixo está o esboço da órbita de um planeta em torno do Sol. A primeira lei de Kepler nos diz que a órbita é uma elipse com o Sol em um dos focos: a, o semi-eixo maior é a distância média do periélio (proximidade do sol) e afélio (distanciamento do sol) do planeta. O período de um planeta (em anos) é dado pela fórmula P = , onde o período P é dado em anos e a é dado em unidades astronômicas (UA).

Exercício

1- Dadas as distâncias do periélio e do afélio dos seguintes planetas, calcular o semi-eixo maior da órbita de cada planeta (em UA) e a duração deste ano ou período (em anos terrestres).

PLANETA	Distância do periélio (UA)	Distância do afélio (UA)	a (em UA)	Período P (em anos)
Mercúrio	0,31	0,47	0,39	0,2435
Vênus	0,720	0,726	0,723	0,6147
Terra	0,98	1,02	1	1
Marte	1,38	1,66	1,52	1,8739
Júpiter	4,95	5,46	5,205	11,8749

2. TRANSFERÊNCIA DE ÓRBITAS

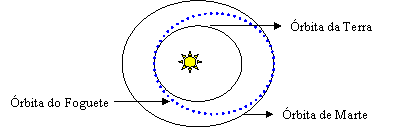
A órbita da nossa nave tripulada que será enviada para Marte também será elíptica, com a órbita da Terra como periélio e a órbita de Marte como afélio. Esta configuração leva ao menor consumo de energia (necessita de menos combustível)

Exercícios

1- Nós vamos tentar lançar nosso foguete para que quando ele alcance Marte, este esteja no periélio. Qual seria a distância do periélio, distância do afélio, o semi-eixo maior (a) e o período P de nosso foguete? (Adote a órbita da Terra circular)

Órbita de Marte

Representação do plano de lançamento:

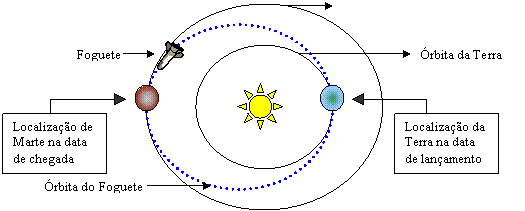
a) A distância do periélio do foguete coincide com o afélio da Terra, que neste caso é 1 UA, pois a órbita da Terra está sendo considerada circular.

b) A distância do afélio do foguete coincide com o periélio de Marte, que neste caso é 1,38UA, pois a órbita de Marte é elíptica.

c) O semi-eixo maior a do foguete é a média do afélio da terra e do periélio de Marte.

Isto é: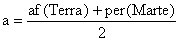

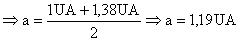
d) O período é dado por 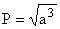onde a é o semi-eixo maior da órbita do foguete, ou seja: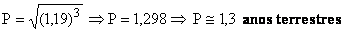

Demonstração:

2- Como nós queremos parar em Marte, o tempo que levaremos para chegar lá é apenas a metade do nosso período orbital em torno do Sol. Quanto tempo (em dias) nós levaremos para chegar a Marte?

O período orbital do foguete é 1,3 anos terrestres. Como o foguete levará metade desse tempo para chegar a Marte, o tempo de viagem será

t = 1,3 anos/2 = 0,65 anos = 237 dias

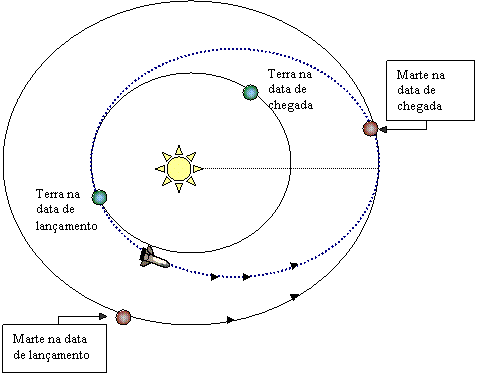
3- Nós decidimos fazer nossa viagem em 2001. Chegando em Marte em 10 de outubro (data aproximada do respectivo ano em que Marte chega ao periélio), em que data nós teremos que partir da Terra?

Vamos primeiro determinar o semi-eixo maior (a) da órbita do foguete. Neste caso, na data do lançamento a Terra encontra-se no afélio, que coincide com o periélio do foguete. Na data de chegada, Marte encontra-se no periélio, logo o foguete estará no afélio.

Então a é media entre o afélio da Terra e o periélio de Marte:

Isto é: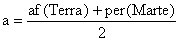

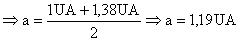
Agora devemos calcular o período orbital do foguete.

Como período é dado por então:

O tempo gasto na 1ª etapa da viagem (ida) é aproximadamente a metade do período orbital do foguete, então o tempo que a nave gastou para chegar a Marte é dado por: 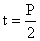, ou seja,

anos.

São 233 dias de viagem

Em 10 de outubro = 280 dias

280 – 233 = 45 dias

jan (31dias) + fev (14dias) = 45

Para saber a data de lançamento, devemos transformar esse tempo em meses e dias e subtrair da data de chegada (10 de outubro).

t = 0,649 x 12

t = 7, 788 meses

t = 7 meses e 23 dias

Data de lançamento: 14 de fevereiro de 2001

4- Nós achamos que não podemos chegar em Marte em 10 de outubro de 2001, porque de acordo com nossos cálculos, na data de lançamento, a posição da Terra não é diametralmente oposta ao Sol de onde Marte estará em 10 de outubro (nossas condições para consumo mínimo de energia). Em vez disso nós partimos em 1° de abril. Agora quando nós chegarmos em Marte ele estará a 1,41 UA do Sol. Em razão de Marte não estar no periélio quando nós chegarmos lá, quanto maior ficará a viagem realizada do que a que nós tínhamos calculado antes (Sugestão: a distância do afélio teve mudanças).

Vamos então determinar o semi-eixo maior (a) da órbita do foguete. Neste caso, na data do lançamento a Terra encontra-se no afélio, que coincide com o periélio do foguete. Na data de chegada, Marte encontra-se no periélio a 1,41UA, logo o foguete estará no afélio.

Então a é a média entre o afélio da Terra e o periélio de Marte:

Isto é: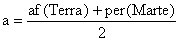

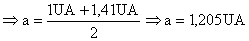
Em seguida calculamos o período.

O período é dado por então:

Como o tempo gasto na 1ª etapa da viagem (ida) é aproximadamente a metade do período orbital, então o tempo que a nave gastou para chegar a Marte é dado por: 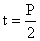, ou seja,

anos.

t = 7 meses e 28 dias.

Se a viagem tivesse sido realizada pelo plano anterior a duração era de 7 meses e 23 dias. Como agora Marte está a uma distância maior que o periélio, então a viagem vai durar mais 5 dias, ou seja, 7 meses e 28 dias.

5- Qual será a data histórica do nosso pouso?

Como ele leva 0,661 anos, convertendo em meses temos 7,932 meses, ou seja, 7 meses e 28 dias.

Em dias esse período equivale a 238 dias. Como a partida ocorreu em 1° de abril, a nave chegará em Marte em 24 de novembro de 2001, pois:

Tempo = 30 (ab) + 31 (ma) + 30 (jun)+ 31 (jul) + 31 (ag) + 30 (set) + 31(out) + 24 (nov)

Tempo = 238 dias

3. VELOCIDADES

A velocidade de um planeta em sua órbita é dada pela fórmula:

onde v é a velocidade, r é a distância (naquele instante) do Sol em UA e a é o semi-eixo maior dessa órbita.

Exercícios

1- Qual é a velocidade na Terra em sua órbita? (Adote uma órbita circular)

Neste caso r é igual a 1UA e a também é igual a 1UA, pois a órbita adotada é circular, então a Terra mantém a distância constante de 1UA do Sol em todo o seu movimento de translação.

A velocidade é dada pela fórmula:

Então:

2- Qual é a velocidade de Marte quando ele está a 1,41 UA do Sol?

Neste caso r é igual a 1,41UA e a é igual a 1,52UA.

A velocidade é dada pela fórmula:

Então:

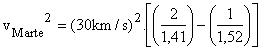
3- Para calcular a velocidade que nossa nave tripulada deveria estar a 1UA, nós determinamos qual a rapidez que ela deve estar se movendo para estar na órbita certa que a levará a Marte. Pela subtração da velocidade da Terra deste número, nós achamos a velocidade que o foguete terá ao estar se movendo relativamente em relação à Terra. Com que velocidade o foguete estará viajando (relativamente a Terra) imediatamente após escapar da gravidade da Terra em direção a Marte como nós planejamos.

Primeiro vamos calcular a velocidade orbital do foguete através da equação:

Agora vamos calcular a velocidade do foguete em relação a Terra:

4- Com que velocidade o foguete estará se movendo com relação a Marte quando ele chegar lá a 1,41 UA?

Como sabemos a velocidade orbital do foguete e a velocidade do planeta Marte, então:

4. COMUNICAÇÃO COM A TERRA

1- Enquanto estivermos na superfície em Marte, nós vamos necessitar manter contato com a Terra e depois da partida também. No nosso ponto mais distante da Terra, Marte estará a mais ou menos 2,66 UA da Terra. Sabendo que 1 UA @ 1,5x10¹³ cm e que nossas ondas de rádio viajam com uma velocidade de 3x10¹⁰ cm/s, quanto tempo nossa mensagem de rádio levará para chegar a Terra deste ponto mais distante?

Como a velocidade de propagação das ondas de rádio é constante, o tempo é dado em função da distância e da velocidade.

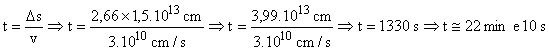
2- Se nós estávamos tentando manter uma conversa com a Terra, quanto tempo nós teríamos que esperar para ouvir a resposta para uma pergunta fácil feita a alguém na Terra?

Como o tempo gasto para que essa onda de rádio atinja esse ponto distante de Marte é de aproximadamente 22 min e 10 s, o tempo que a mensagem de resposta aqui da Terra chegue a Marte será aproximadamente igual, logo, o tempo total é de @ 45 min.

5. RETORNO

Nós simplesmente não podemos retornar no momento que nós gostaríamos. Teremos que esperar para partir (com o objetivo de economizar combustível) até que a Terra esteja na posição adequada no final da nossa transferência de órbita para casa. Em geral, têm se ai uma longa espera, mas nós levamos reservas suficientes para fazer isto do começo ao fim (enquanto isso nós podemos explorar Marte).

1- O cálculo do tempo exato que nós teremos que esperar é complicado, mas nós podemos colocar um limite máximo sobre ele na realização desta viagem, que depois de um período sinódico a Terra estará em algum lugar, relativo a Marte, como ele estava quando nós pousamos. Certamente os dois planetas seguirão suas trajetórias antes de lançarmos e depois.

Usando a fórmula:

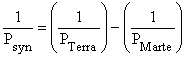
calcule qual seria o período sinódico (ou seja, o longo tempo de espera)

Onde P_Syn é o período sinódico.

Período sinódico: é o intervalo de tempo decorrido entre duas configurações iguais consecutivas. É o período de revolução aparente do planeta, em relação à Terra.

O período terrestre é 1 e o período marciano é 1,87 anos terrestre, então:

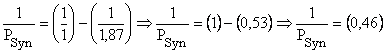
2- Nós finalmente chegamos em casa com amostras, fotos, etc. Considerando que tivemos que esperar ¾ de período sinódico antes de sair de Marte, quanto tempo ao todo durou nossa viagem?

Como a espera foi de ¾ de períodos sinódico, então, podemos converter isso para anos terrestres através da relação:

---

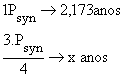
[1] Tradução livre do exercício “Interplanetary Travel” proposto no livro “Introductory Astronomy Exercises”, de Dale C. Ferguson (1990).