O Movimento de Rotação é a revolução de um corpo celeste sobre seu próprio eixo (imaginário). O tempo gasto para realizar esse percurso é chamado de período .

Embora esse movimento se aplique aos demais planetas do Sistema Solar, vamos limitar o nosso estudo ao Planeta Terra.

O período da Terra no seu movimento de Rotação é de aproximadamente 1 dia (23 h e 56 minutos). Esse valor foi obtido observando o movimento do Sol em relação ao horizonte.

Fazendo uma hipótese simplificada de que o movimento de rotação da Terra é um movimento circular uniforme podemos obter a velocidade angular da Terra pela equação:

Onde w é a velocidade angular, 2 p é o ângulo descrito em uma volta completa e T é o período.

Considerando o período da Terra como 24 h, a sua velocidade angular será:

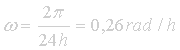
Observe que para todos os pontos da Terra a velocidade angular é a mesma já que o período no Movimento de Rotação da Terra é igual em qualquer lugar.

Considerando o raio da Terra R e o seu período T, podemos determinar o módulo da velocidade linear V de um ponto situado na superfície da Terra em função do Movimento de Rotação pela equação:

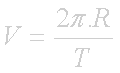
Considerando um ponto no equador (R = 6.400 km) e o período aproximado de rotação (T = 24 h), obtemos:

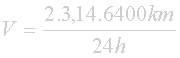
Resolvendo, obtemos para a velocidade da Terra aproximadamente 1675 km/h que equivale a aproximadamente 465 m/s.

Para um ponto situado no equador terrestre, a distância ao eixo de rotação coincide com o raio da Terra. Para outros pontos na superfície da Terra, que não estão no equador teremos velocidades lineares menores. Procure entender o fato, olhando a figura abaixo.

No equador a latitude á zero. Para outros pontos situados acima ou abaixo do equador, a distância ao eixo de rotação da Terra é menor. Lembrando que a latitude de um local da Terra é o ângulo medido desde a linha do equador até o lugar, pode-se conhecendo a latitude, determinar a distância do lugar ao eixo de rotação da Terra. Conforme aumenta a latitude, diminui a distância do ponto ao eixo de rotação da Terra e também a velocidade linear, já que esta é proporcional à distância.

Na tabela abaixo, temos os valores de velocidades de pontos situados em 3 cidades brasileiras. Você pode conferir os valores, aplicando os valores das distâncias na equação da velocidade linear. Veja que, quanto menor a distância da cidade ao eixo de rotação localizado no centro da Terra, menor é a velocidade linear.

Isso vale para o movimento de rotação de corpos rígidos, onde a velocidade angular é constante e conseqüentemente a velocidade linear é diretamente proporcional ao raio.

Corpos não rígidos em geral tem rotação diferencial, isto é, com velocidade angular não constante; nesses corpos em geral a velocidade é maior quanto mais próximo o ponto estiver do eixo de rotação, diminuindo para pontos mais afastados do eixo de rotação. Se a velocidade angular diminui consequentemente a velocidade linear tabém diminui.

O movimento de translação dos planetas em torno do Sol tem esse comportamento. Por isso esse tipo de comportamento é chamado Kepleriano. Confirme a veracidade dessas afirmativas nas Leis de Kepler.

Os dias e as noites são uma conseqüência do movimento de rotação da Terra.

O movimento do Sol, de Leste para Oeste, que observamos durante o dia é um reflexo do movimento de rotação da Terra, de Oeste para Leste.