Exercícios


  1. Calcule a massa do Sol a partir do movimento da Terra em torno dele.
  2. Calcule o raio do Sol a partir de seu diâmetro angular de 0,5o, e de sua distância à Terra de 150 milhões de km.
  3. Calcule a densidade média do Sol.
  4. A partir do deslocamento Doppler das linhas espectrais da luz provinda dos limbos leste e oeste do Sol, encontra que as velocidades radiais dos dois limbos diferem por 4 km/s. Encontre o período aproximado de rotação do Sol.
    DICA:
    se as velocidades dos dois limbos diferem por 4km/s, a velocidade de rotação de um ponto na superfície do Sol é 2 km/s. O Raio do Sol é 696000 km.
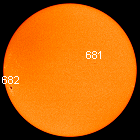
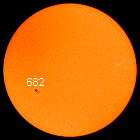
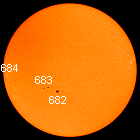
  5. As figuras abaixo são fotos do sol em 4 dias de outubro de 2004: 14,16,18 e 20. A partir do movimento da mancha 682, meça o período de rotação do sol no paralelo dessa mancha. Compare com a resposta do exercício anterior.
    DICA:
    Para isso você deve imprimir as fotos e medir com uma régua quantos cm a mancha no intervalo de tempo decorrido. Determine a escala km/cm de cada imagem do Sol usando o raio do Sol dado na questão anterior. O arco (a) percorrido pela mancha nesse intervalo de tempo (Δt) é subentendido por um ângulo (θ), no centro do Sol, tal que sen θ/2 = a/(2R), onde R é o raio do paralelo da mancha (que é um pouco menor do que o raio equatorial porque a mancha está abaixo do equador). Como um determinado ponto na superfície do Sol dá uma volta completa (360 graus) em um período de rotação (P), então o período do Sol pode ser encontrado pela relação: P/360 = Δt/ θ
  6. Os grânulos da fotosfera solar, têm diâmetro de 1 segundo de arco. Também são observados supergrânulos com diâmetros de até 1 minuto de arco. A quantos quilômetros correspondem estas estruturas? Compare com o diâmetro da Terra.
    DICA: Os grânulos apresentam diâmetro de 1 segundo de arco quando observados da Terra, que está a uma distância de 150 milhões de km do Sol.
  7. No dia 20/10/2004, o site http://www.spaceweather.com reporta os seguintes dados sobre o vento solar: velocidade de 437 km/s, e densidade de 6,8 prótons/cm3. Assumindo que esses dados representam valores típicos, calcule
    1. o fluxo de prótons que chega à Terra (cm-2 s-1). DICA: o fluxo de prótons é obtido multiplicando a velocidade do vento solar pela densidade do vento.
    2. o no. total de prótons que sai do Sol por segundo
    3. a massa perdida pelo Sol devido ao vento solar, em kg/s e em Msolar/ano
    4. Verifique no site mencionado acima os dados do vento solar para hoje, e compare-os com os usados nos cálculos deste exercício.
  8. O que é a "constante solar"? Quanto ela vale? Qual seria o seu valor em Saturno, que est´ a 10 UA do Sol?
  9. A principal fonte de energia das estrelas é a reação termonuclear de fusão de 4 núcleos de hidrogênio em um núcleo de hélio. Mostre que nesse processo existe uma "sobra" de 0,7% da massa, que se transforma em energia.
    10. -->
  10. Encontre o fluxo de radiação na superfície do Sol, lembrando que o fluxo de radiação solar que chega à Terra, é 1390 W/m2 (constante solar).
  11. Calcule a luminosidade do Sol (energia por segundo que ele emite).
  12. Supondo que o Sol permanecerá estável atá ter usado 10% de sua massa na fusão de H em He, e assumindo que ele já fundiu 5% dessa massa, calcule quanta energia o Sol ainda tem para liberar de forma estável. (Lembre que na transformação de H em He apenas 7% da massa se transforma em energia).
  13. Calcule o tempo de vida estável que o Sol ainda tem, supondo que sua luminosidade durante esse tempo permanece constante e igual ao valor atual (calculado dois ítens acima).
  14. Quando o Sol chegar a o final de sua vida ele será uma anã branca, como massa de aproximadamente 0,6 massas solares e raio de aproximadamente 10 mil km. Calcule qual será então sua densidade, sua gravidade superficial e a velocidade de escape em sua superfície.
Use a equação de equilíbrio hidrostático para :
  1. Mostrar que a pressão, Pc, no centro de uma estrela de densidade uniforme r , com raio R e massa M, é proporcional a:

    Pc ∝ r M
    R
    ou
    Pc ∝ M2
    R4
    [Substitua dP/dr por DP/Dr, e use Dr como o intervalo entre r = 0 e r = R. Assuma que P(r = R) é desprezável comparado com Pc.]
  2. a pressão central do Sol é

    Pc ∝ 1014 N m-2
  • O livre caminho médio de um fóton é dado por

    d = 1/kr
    k e r são, respectivamente, o coeficiente de absorção de massa do fóton e a densidade do meio.
    1. Sabendo que o coeficiente de absorção de massa do fóton no interior do Sol é k = 10  m2 kg-1, encontre o livre caminho médio do fóton dentro do Sol.
    2. Embora o raio do Sol seja aproximadamente R = 109 m, pode-se mostrar que o caminho total percorrido por um fóton dentro do Sol é s = [(R2)/d] = 1022 m. Calcule quanto tempo o fóton leva para viajar desde o centro do Sol até sua superfície.
    3. Sabendo que o coeficiente de absorção de massa do neutrino é k = 10 -21 m2 kg-1, encontre o livre caminho médio do neutrino no centro do Sol, e quanto tempo o neutrino leva para viajar desde o centro do Sol até sua superfície, assumindo que ele viaja à velocidade da luz.
    • O Sol e as outras estrelas:

    O Sol e as outras estrelas:

    Distâncias, propriedades principais, fonte de energia e tempo de vida
    1. Mostre que um parsec é igual a 3,086 ×1013 km, e que também é igual a 3,26 anos-luz.
    2. Próxima Centauri tem uma paralaxe heliocêntrica de 0,76 segundos de arco.
      1. Qual sua distância em parsecs? Em anos-luz?
      2. Qual seria a paralaxe de Próxima Centauri para um habitante de Marte?
    3. Uma estrela tem magnitude aparente m=1.
      1. Quantas vêzes mais fraca ela ficaria se estivesse ao triplo de sua distância?
      2. Quantas magnitudes mais fraca ela apareceria?
    4. Considere um sistema binário em que cada estrela tem a massa do Sol e a distância média entre as duas é de 2 UA.
      1. Qual o seu período orbital?
      2. A que distância as duas estrelas pareceriam ter uma separação angular de 1¢¢?
    5. Duas estrelas de tamanhos iguais estão à mesma distância da Terra. Uma tem temperatura de 5800 K e a outra tem temperatura de 2900 K.
      1. Qual a mais vermelha? Qual a mais azul?
      2. Em que comprimento de onda cada uma emite o máximo de radiação?
      3. Calcule a razão entre o fluxo das duas que chega à Terra.
      4. Qual a diferença de magnitude entre as duas?
    6. A distância do Sol à Terra, definida como Unidade Astronômica (UA), é de 150 milhões de quilômetros, e sua magnitude aparente, da Terra, é em torno de -26.
      1. Quanto vale a distância do Sol, em parsecs?
      2. Qual é a magnitude aparente do Sol visto de Saturno, que está a @ 10 UA de distância do Sol?
    7. Ainda sobre o Sol:
      1. Calcule a sua massa, a partir do movimento da Terra em torno dele.
      2. Calcule o seu raio real, assumindo que seu raio angular visto da Terra é de 0,5o, e que sua distância à Terra é 150 milhões de km.
      3. Calcule a sua densidade média.


      File translated from TEX by TTH, version 3.54.
      On 13 Jul 2004, 17:36.

      File translated from TEX by TTH, version 3.54.
      On 20 Oct 2004, 17:06.       -->