A viscosidade dos líquidos vem do atrito interno, isto é, das forças de coesão entre moléculas relativamente juntas. Desta maneira, enquanto que nos gases a viscosidade cresce com o aumento da temperatura, nos líquidos ocorre o oposto. Com o aumento da temperatura, aumenta a energia cinética média das moléculas, diminui (em média) o intervalo de tempo que as moléculas passam umas junto das outras, menos efetivas se tornam as forças intermoleculares e menor a viscosidade.
A tabela abaixo indica o coeficiente de viscosidade para alguns fluidos:
|
Líquidos
(10-1Pa.s)
|
Gases
(10-7 Pa.s)
|
| Glicerina (20 °C) |
8,3
|
Ar (0 °C) |
171
|
| Água (0 °C) |
0,0179
|
Ar (20 °C) |
181
|
| Água(100 °C) |
0,0028
|
Ar (100 °C) |
218
|
| Éter (20 °C) |
0,0124
|
Água (100 °C) |
132
|
| Mercúrio (20 °C) |
0,0154
|
CO2 (15 °C) |
145
|
Consideremos uma esfera de raio R movendo-se através de um fluido com uma velocidade constante.

Então, sobre esta esfera existe uma força de resistência , exercida pelo fluido, cujo módulo depende do coeficiente de viscosidade h do fluido, do raio R da esfera e do módulo v de sua velocidade (se este é pequeno). Como a única maneira pela qual estas grandezas podem ser combinadas para que o resultado tenha dimensão de força é no produto hRv, temos:
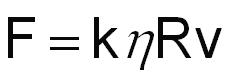
onde k é uma constante adimensional.
Pela análise física deste problema, Stokes descobriu que esta constante vale 6p. Assim, o módulo da força de resistência do fluido sobre a esfera se escreve (lei de Stokes):
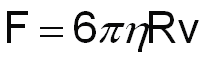
É interessante notar que se as gotas de chuva provenientes de nuvens situadas a alguns quilômetros de altura não encontrassem a resistência do ar, elas seriam extremamente danosas ao atingir qualquer corpo na superfície da Terra. Isto não acontece porque elas alcançam uma velocidade terminal pequena. Para gotas de 1 mm de diâmetro, esta velocidade é cerca de 4,3 m/s e para gotas de 2 mm de diâmetro, esta velocidade é cerca de 5,8 m/s.