No movimento circular o vetor velocidade varia, de tal forma que podemos calcular a aceleração fazendo a razão entre a variação vetorial da velocidade pelo tempo decorrido.
Considerando qua a variação de velocidade num intervalo de tempo muito pequeno, ou seja, quando delta t tende a zero, a aceleração calculada será a aceleração instantânea.
Observe as figuras:
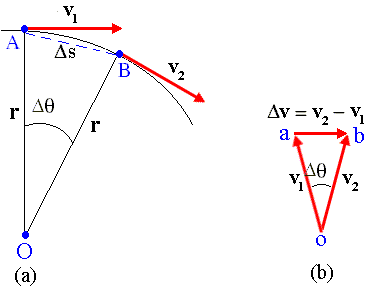Da figura (a), se unirmos pela origem os vetores v1 e v2 obteremos
a soma vetorial pelo segmento ab como mostra a figura (b).
Os triângulos OAB e oab, nas figuras (a) e (b) são semelhantes e, portanto podemos afirmar que o deslocamento do móvel está para o raio da circunferência assim como a variação de velocidade está para a velocidade inicial.
Dividindo ambos os termos da equação pela variação no tempo teremos, no primeiro membro, a aceleração. E, considerando que, a aceleração instantânea no determinado ponto é o valor limite desta expressão quando B tende para A, de forma que v1 pode ser representado por v, a equação fica:
NOTA: A aceleração centrípeta pode ser calculada por acp = v2 / r
e também pela equação: acp = omega2 . r pois v = omega . r